Die Kaplan-Meier-Kurve ist ein grafisches Darstellungsinstrument, das in der Überlebensanalyse verwendet wird, um die Überlebenszeit von Patienten oder die Zeit bis zum Auftreten eines Ereignisses darzustellen. Die Kurve zeigt die Wahrscheinlichkeit an, dass ein Patient innerhalb eines bestimmten Zeitraums überlebt oder bis zu einem bestimmten Ereignis ohne Auftreten des Ereignisses verbleibt.

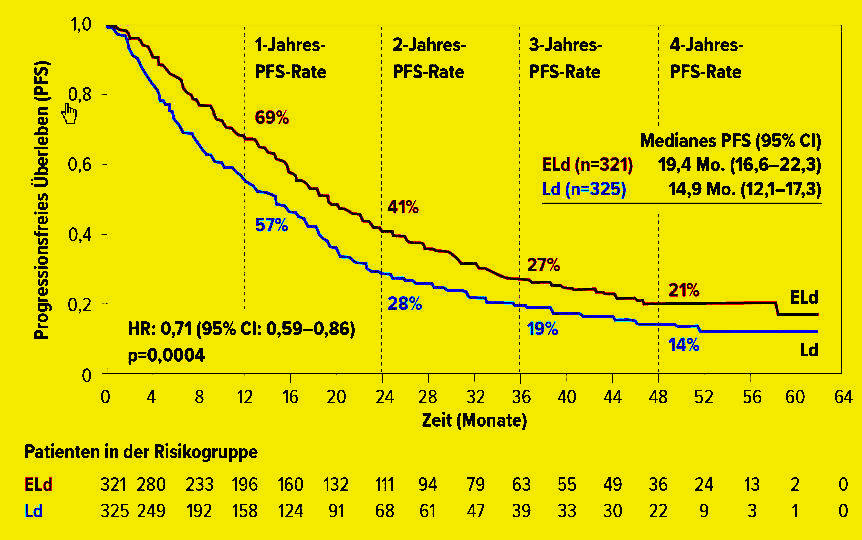
Die Kaplan-Meier-Kurve wird erstellt, indem die Überlebenszeit oder die Zeit bis zum Ereignis für jeden Patienten in einer Gruppe (z.B. einer Behandlungsgruppe oder einer Kontrollgruppe) erfasst wird. Die Überlebenszeit wird in Intervalle unterteilt, und für jedes Intervall wird die Anzahl der Patienten berechnet, die das Ereignis erlebt haben oder nicht.

Die Kurve beginnt bei 100 % Überleben oder Ereignisfreiheit zu Beginn der Studie und fällt mit der Zeit ab, um die Proportion der Patienten darzustellen, die das Ereignis erlebt haben. Die Steigung der Kurve gibt an, wie schnell Patienten das Ereignis erleben, und die Abstände zwischen den Kurven zeigen Unterschiede zwischen den Gruppen.

Die Kaplan-Meier-Kurve ist ein wichtiges Instrument in der klinischen Forschung, da sie es ermöglicht, die Überlebenszeit von Patienten und den Effekt von Behandlungen quantitativ darzustellen und zu vergleichen. Sie kann auch zur Identifizierung von Risikofaktoren und zur Entwicklung von Prognosen verwendet werden.

Es ist wichtig zu beachten, dass die Kaplan-Meier-Kurve ein statistisches Instrument ist und nur eine Schätzung der Überlebenszeit oder des Ereignisrisikos darstellt. Die Interpretation der Kurve erfordert daher auch die Berücksichtigung anderer Faktoren wie der Stichprobengröße, der Follow-up-Zeit und der Varianz in der Überlebenszeit.

Die Hazard Ratio (HR) ist ein statistisches Maß, das in der Überlebensanalyse verwendet wird, um den Unterschied in der Zeit bis zum Auftreten eines Ereignisses (z.B. Tod, Rückfall, Krankheitsprogression) zwischen zwei Gruppen zu messen. Es gibt an, wie viel größer oder kleiner das Risiko ist, dass ein Ereignis in einer Gruppe auftritt, verglichen mit der anderen Gruppe.

Eine Hazard Ratio von 1,0 bedeutet, dass die Ereignisraten in beiden Gruppen gleich sind. Eine HR von mehr als 1,0 bedeutet, dass das Risiko, ein Ereignis in der behandelten Gruppe zu erleiden, höher ist als in der Kontrollgruppe, während eine HR von weniger als 1,0 darauf hinweist, dass das Risiko in der behandelten Gruppe niedriger ist.

Ein Beispiel: Angenommen, eine klinische Studie vergleicht die Überlebenszeit von Patienten mit einem bestimmten Krebs, die entweder eine neue Behandlung oder eine Standardbehandlung erhalten haben. Wenn die Hazard Ratio 0,7 beträgt, bedeutet dies, dass das Risiko, an Krebs zu sterben, bei den Patienten, die die neue Behandlung erhalten haben, um 30 % niedriger ist als bei den Patienten, die die Standardbehandlung erhalten haben.

Die Hazard Ratio ist ein wichtiges statistisches Maß in der klinischen Forschung, da sie die Effektivität von Behandlungen quantifiziert und die Entscheidungsfindung in der medizinischen Praxis beeinflussen kann.

Der p-Wert (auch Signifikanzniveau genannt) ist ein statistisches Maß, das in klinischen Studien verwendet wird, um zu beurteilen, ob ein Unterschied zwischen zwei Gruppen signifikant ist oder nur aufgrund des Zufalls auftritt. Der p-Wert gibt die Wahrscheinlichkeit an, dass die beobachteten Unterschiede zwischen den Gruppen auf Zufall beruhen, wenn tatsächlich kein Unterschied besteht.

Ein p-Wert kleiner als 0,05 (oder 0,01) wird oft als Schwellenwert angesehen, um den Unterschied als statistisch signifikant zu betrachten. Das bedeutet, dass es weniger als 5 % (oder 1 %) Wahrscheinlichkeit gibt, dass der beobachtete Unterschied allein auf Zufall beruht. Ein p-Wert größer als 0,05 bedeutet, dass der Unterschied nicht signifikant ist und möglicherweise auf Zufall oder andere Faktoren zurückzuführen ist.

Es ist jedoch wichtig zu beachten, dass der p-Wert nicht allein ausreicht, um die klinische Bedeutung eines Ergebnisses zu bewerten. Ein kleiner p-Wert bedeutet nicht unbedingt, dass der beobachtete Unterschied zwischen den Gruppen klinisch bedeutsam ist oder dass die Behandlung tatsächlich effektiv ist. Andere Faktoren wie die Stärke des Effekts, die Größe der Stichprobe, die klinische Relevanz des Ergebnisses und die Sicherheit der Behandlung müssen ebenfalls berücksichtigt werden.

Insgesamt ist der p-Wert ein wichtiger statistischer Parameter, der dazu beiträgt, die Gültigkeit und Relevanz von Ergebnissen in klinischen Studien zu bewerten.

Ein Konfidenzintervall oder Vertrauensbereich ist ein statistisches Maß für die Unsicherheit oder Variabilität, die in einer Schätzung eines Parameters (z.B. Mittelwert, Hazard Ratio) enthalten ist. Es gibt an, wie sicher wir sind, dass der wahre Wert des Parameters innerhalb des Intervalls liegt.

Ein Konfidenzintervall wird oft mit einem Konfidenzniveau angegeben, das angibt, wie oft das Intervall den wahren Wert des Parameters umschließt. Ein Konfidenzniveau von 95 % bedeutet zum Beispiel, dass bei wiederholter Anwendung des Schätzverfahrens in 95 % der Fälle das Konfidenzintervall den wahren Wert des Parameters enthält.